1.前言

决策树就是一棵树，一颗决策树包含一个根节点、若干个内部结点和若干个叶结点；叶结点对应于决策结果，其他每个结点则对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果被划分到子结点中；根结点包含样本全集，从根结点到每个叶子结点的路径对应了一个判定测试序列。
如下图所示，根据水果的属性（颜色、形状、直径）来判断水果的种类。

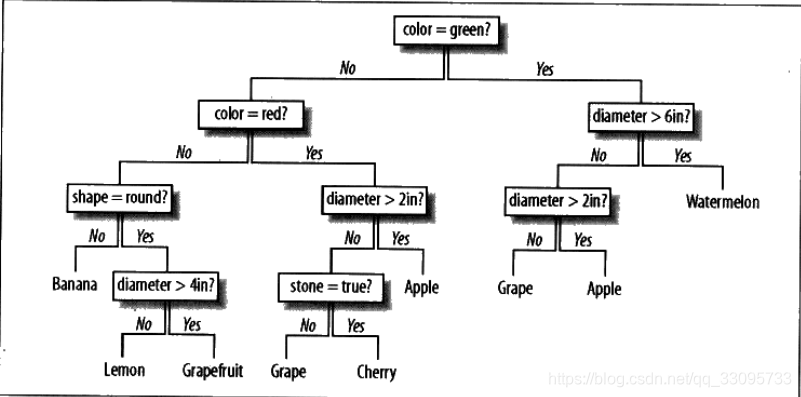
在这里插入图片描述

决策树可以同时接受分类数据，如颜色、形状，和数值数据，如直径，作为输入。决策树对于只包含几种可能结果的问题而言，处理起来非常高效，但是面对拥有大量可能结果的数据集时，算法效率就好降低。

2.决策树的建立

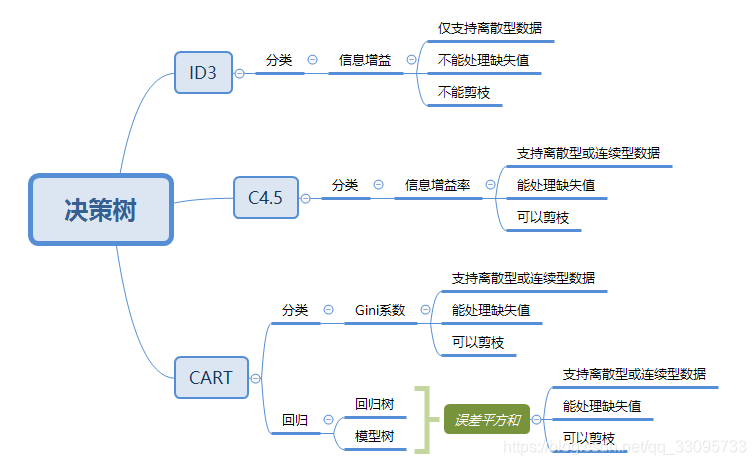
决策树的训练算法有三种CART、ID3和C4.5。CART必须是二叉树，而ID3和C4.5，不一定是二叉树。决策树学习的关键在于如何选择最优的划分属性，所谓的最优划分属性。最优特征选择方法分为基尼不纯度、信息增益、信息增益率三种。在ID3算法中我们使用了信息增益来选择特征，信息增益大的优先选择。在C4.5算法中，采用了信息增益比来选择特征，以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的，这里面会涉及大量的对数运算。CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的。

在这里插入图片描述

2.1 CART训练算法

Scikit-Learn使用的是分类与回归树（Classification And Regression Tree，简称CART）算法来训练决策树（也叫作“生长”树）。想法非常简单：首先，使用单个特征k和阈值tk（例如，花瓣长度≤2.45厘米）将训练集分成两个子集。k和阈值tk怎么选择？答案是产生出最纯子集（受其大小加权）的k和tk。算法尝试最小化的成本函数为。
在这里插入图片描述

左右子集的不纯度就可以采用基尼不纯度或者信息增益。

默认使用的是基尼不纯度来进行测量，但是，可以将参数criterion设置为”entropy”来选择信息熵作为不纯度的测量方式。熵的概念源于热力学，是一种分子混乱程度的度量：如果分子保持静止和良序，则熵接近于零。后来这个概念传播到各个领域，其中包括香农的信息理论，它衡量的是一条信息的平均信息内容：如果所有的信息都相同，则熵为零。在机器学习中，它也经常被用作一种不纯度的测量方式：如果数据集中仅包含一个类别的实例，其熵为零。

数据集D的纯度可用基尼值来度量

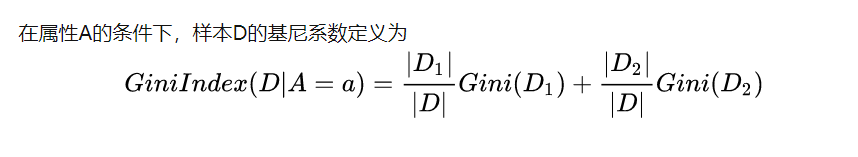
在这里插入图片描述

数据集的属性有3个，分别是有房情况，婚姻状况和年收入，其中有房情况和婚姻状况是离散的取值，而年收入是连续的取值。拖欠贷款者属于分类的结果。

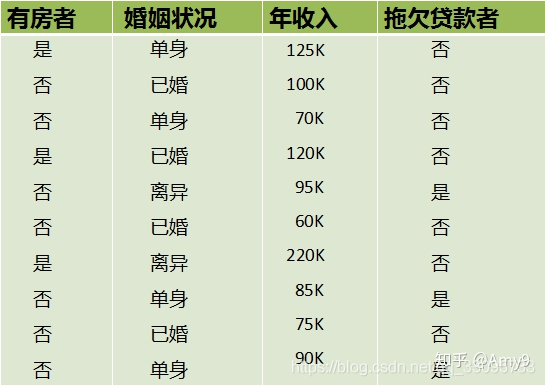
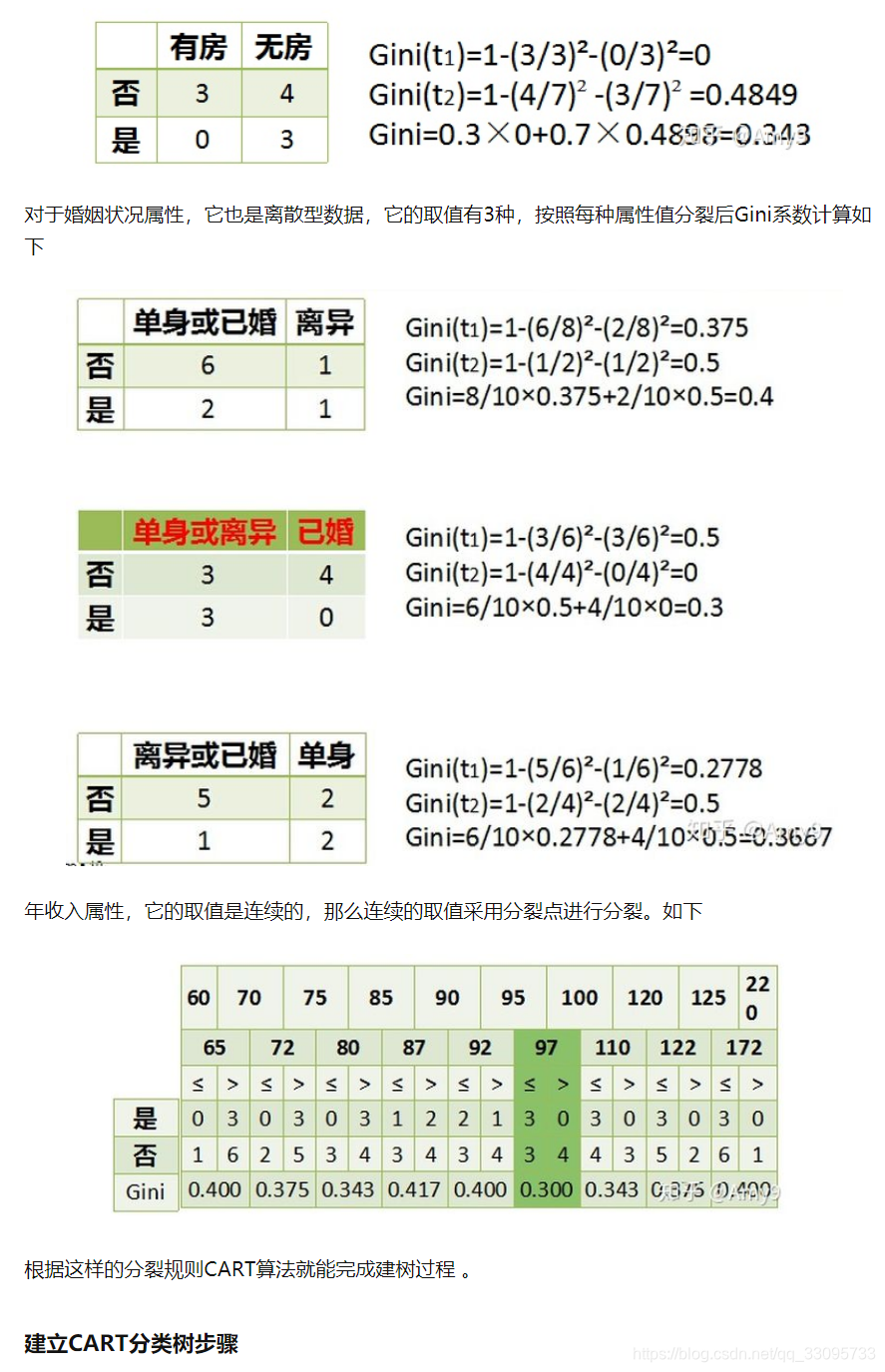
在这里插入图片描述

对于有房情况这个属性，它是离散型数据，那么按照它划分后的Gini系数计算如下。

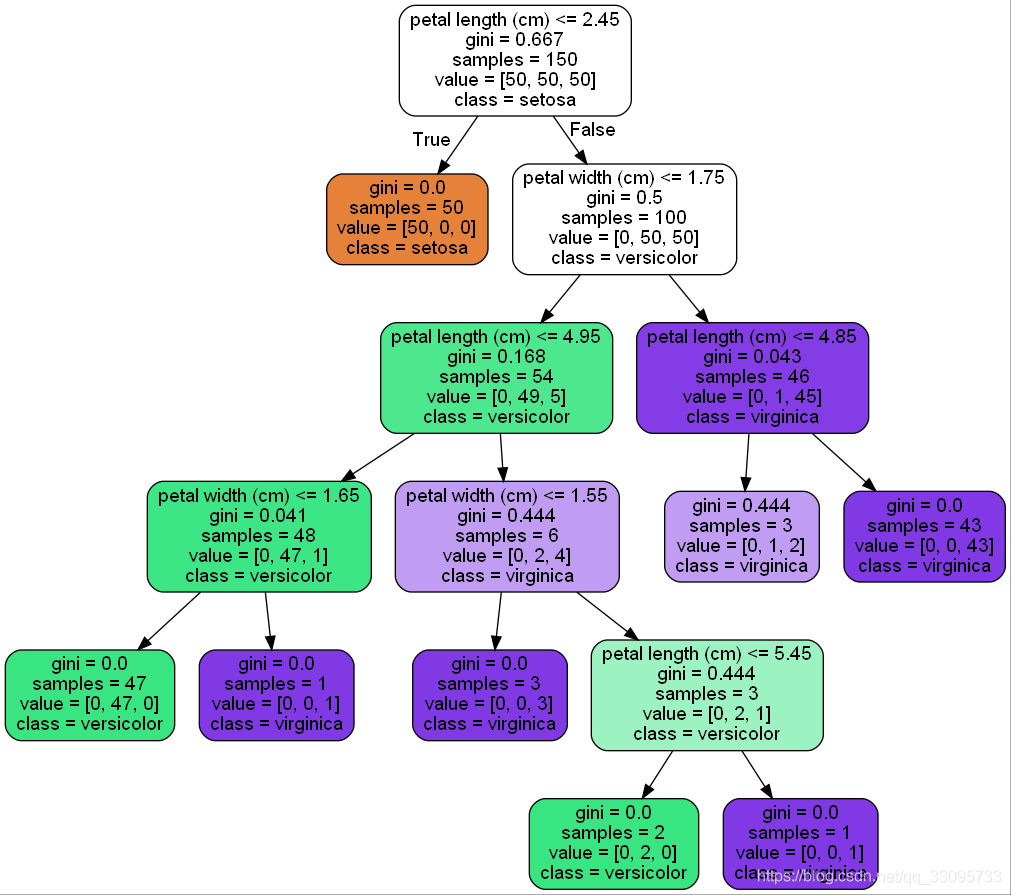
在这里插入图片描述

使用sklearn对iris数据集建立决策树代码如下：


from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz

from sklearn import svm
import numpy as np


if __name__ == '__main__':
    iris = datasets.load_iris()

    x = iris.data[:,2:]
    y = iris.target

    tree_clf = DecisionTreeClassifier()
    tree_clf.fit(x,y)

    export_graphviz(
        tree_clf,
        out_file="iris_tree.dot",
        feature_names=iris.feature_names[2:],
        class_names=iris.target_names,
        rounded=True,
        filled=True
    )